Search

Graph Theory Part-1

Upendra Upadhyay
May 26, 2017
5 min read

Hi , In this Article We are going to talk about Graph and It's Implementation.

Graph is a data structure that consists of following two components: 1. A finite set of vertices also called as nodes.(V = {v1, v2, v3, v4......}) and 2. A finite set of ordered pair of the form (u, v) called as edge.

The pair is ordered because (u, v) is not same as (v, u) in case of directed graph(di-graph). The pair of form (u, v) indicates that there is an edge from vertex u to vertex v. The edges may contain weight/value/cost.

Consider a graph, G in Fig. 9.1. Then the vertex V and edge E can be represented as: V = {v1, v2, v3, v4, v5, v6} and E = {e1, e2, e3, e4, e5, e6} E = {(v1, v2) (v2, v3) (v1, v3) (v3, v4), (v3, v5) (v5, v6)}. There are six edges and vertex in the graph

Use of Graph

Graphs are used to represent many real life applications: Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, facebook. For example, in facebook, each person is represented with a vertex(or node). Each node is a structure and contains information like person id, name, gender and locale. See this for more applications of graph

BASIC TERMINOLOGIES

A directed graph G is defined as an ordered pair (V, E) where, V is a set of vertices and the ordered pairs in E are called edges on V. A directed graph can be represented geometrically as a set of marked points (called vertices) V with a set of arrows (called edges) E between pairs of points (or vertex or nodes) so that there is at most one arrow from one vertex to another vertex. For example, Fig shows a directed graph, where G = {a, b, c, d }, {(a, b), (a, d), (d, b), (d, d), (c, c)}

An edge (a, b), in said to the incident with the vertices it joints, i.e., a, b. We can also say that the edge (a, b) is incident from a to b.

The vertex a is called the initial vertex and the vertex b is called the terminal vertex of the edge (a, b).

If an edge that is incident from and into the same vertex, say (d, d) of (c, c) in Fig., is called a loop.

Two vertices are said to be adjacent if they are joined by an edge. Consider edge (a, b), the vertex a is said to be adjacent to the vertex b, and the vertex b is said to be adjacent from the vertex a.

A vertex is said to be an isolated vertex if there is no edge incident with it In Fig. 9.vertex C is an isolated vertex

An undirected graph G is defined abstractly as an ordered pair (V, E), where V is a set of vertices and the E is a set at edges.

An undirected graph can be represented geometrically as a set of marked points (called vertices) V with a set at lines (called edges) E between the points. An undirected graph G is shown in Fig.

A graph G is said to be weighted graph if every edge and/or vertices in the graph is assigned with some weight or value.

A weighted graph can be defined as G = (V, E, We, Wv) where V is the set of vertices, E is the set at edges and We is a weights of the edges whose domain is E and Wv is a weight to the vertices whose domain is V. Consider a graph In Fig 9:6 which shows the distance in km between four metropolitan cities in India. Here V = {N, K, M, C,} E = {(N, K), (N,M,), (M,K), (M,C), (K,C)} We = {55,47, 39, 27, 113} and Wv = {N, K, M, C} The weight at the vertices is not necessary to maintain have become the set Wv and V are same. An undirected graph is said to be connected if there exist a path from any vertex to any other vertex. Otherwise it is said to be disconnected.

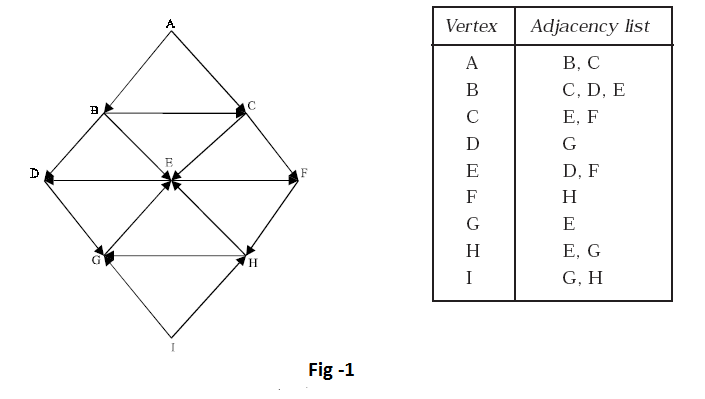
REPRESENTATION OF GRAPH Graph is a mathematical structure and finds its application is many areas, where the problem is to be solved by computers. The problems related to graph G must be represented in computer memory using any suitable data structure to solve the same. There are two standard ways of maintaining a graph G in the memory of a computer. 1. Sequential representation of a graph using adjacent(Adjaceny Matrix) 2. Linked representation of a graph using linked list(Adjaceny List)

Adjacency Matrix: Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.

The adjacency matrix A of an undirected graph G = (V, E) can be represented (in Fig below) with the following conditions Aij = 1 {if there is an edge from Vi to Vj or if the edge (i, j) is member of E} Aij = 0 {if there is no edge from Vi to Vj or the edge i, j, is not a member of E}

Pros: Representation is easier to implement and follow. Removing an edge takes O(1) time. Queries like whether there is an edge from vertex ‘u’ to vertex ‘v’ are efficient and can be done O(1).

Cons: Consumes more space O(V^2). Even if the graph is sparse(contains less number of edges), it consumes the same space. Adding a vertex is O(V^2) time

Lets Code it

package com.graphdemo; import java.util.Scanner; public class Graph { private int vertices; //define no of verices private int [][]adj_matrix; // for representation of Adcency Matrix public Graph(int vertices) { //intialize Graph with Vertices Count this.vertices=vertices; adj_matrix=new int[vertices][vertices]; } public void addEdges(int i, int j, int w) { //add weight to edges if(i>=0&&i<vertices&&j>=0&&j<vertices) adj_matrix[i][j]=w; } public int getEdges(int i,int j) { // return weight of edges return adj_matrix[i][j]; } public static void main(String[] args) { Scanner sc=new Scanner(System.in); System.out.println("enter no of vertices you want"); int v=sc.nextInt(); System.out.println("enter no of edges you want"); int e=sc.nextInt(); Graph g=new Graph(v); for (int i = 0; i < e; i++) { System.out.println("add Edges"); //add i ,j,and weight g.addEdges(sc.nextInt(), sc.nextInt(), sc.nextInt()); } //Print graph........................ System.out.println(); for (int i = 0; i < v; i++) { System.out.print("|"+i+ " |"); for (int j = 0; j < v; j++) { System.out.print(g.getEdges(i, j)+ " "); } System.out.println(); } } }